International C2 Journal: Issues

Vol 1, No 1 (2007)

NOTE: The equations in this article may not appear correctly in some versions of Microsoft Internet Explorer. If you experience this problem, you may read the article in PDF form.

Modelling Human Decision-Making in Simulation Models of Conflict

James Moffat (Senior Fellow, Dstl, UK)

Abstract

The development of Network Enabled Capability (NEC) is one of the key priorities for the UK Ministry of Defence. It is both a difficult and highly important problem for our customer community. I have thus been working on issues related to NEC (and precursor UK concepts such as Digitisation of the Battlespace) for a number of years. At its core is an understanding of how better information and a better approach to Command and Control (C2) lead to both better decisions and improved execution (or operations).

My research on this subject has split fairly well into two parts:

developing a conceptual understanding of and improved approaches to Command and Control (thus assisting the development of doctrine) and
developing quantified Operational Analysis (OA) models to allow assessment of cost-benefit, and balance of investment across the defence budget.

From the start, I took a new approach to the representation of Command and Control, based on the understanding from Complexity Theory that simpler agents, joined in a network or hierarchy, can represent the key effects of higher level Command and Control. This key insight (which actually pre-dates the formal development of Complexity Theory) has led to the conceptualization of the Deliberate and Rapid Planning processes, and the development of a new generation of simulation models which now underpin Dstl’s ability to analyse balance of investment across the equipment budget (including sensors and command systems), future force structures, and the implications of high level Defence policy. This approach, involving two canonical planning processes has also stimulated other developments such as the JOCASTS wargame used by the UK Joint Services Command and Staff Course (JSCSC at the Defence Academy), and the HiLOCA model (now owned by Qinetiq).

These models can be seen as very abstract, and far removed from the actual practice of command in the field. In order to show how they do indeed reflect real aspects of human decision-making, I go on to discuss some of our experimental data which have helped to test and validate these models. I also describe some underpinning studies of the nature of command decision-making in experimental situations, including some recent work looking at the nature of human decision-making in CBRN[1] commanders. Our focus here is mainly on capturing the decision-making of a commander, supported by his or her staff. Of course, in the simulation environment, we also have to capture the way in which such commanders interact with each other in organizations or coalitions. Finally, I assess our ability to understand and model network-centric approaches to command and control and identify some areas that need further work.

Introduction

I want to start by discussing some background ideas which have helped to shape the direction of my work. Cybernetics[2] is the science of control and communication in the animal and in the machine, as defined by Norbert Wiener (Weiner 1948). It can thus offer up some fundamental insights into the subject of human command and decision-making. A basic concept in Cybernetics is ‘variety’ (the number of different accessible states of a system, and thus a measure of potential system agility). In particular, Ashby’s Law of Requisite Variety, discussed in (Atkinson and Moffat 2005), indicates that for a system to be in control, the variety of the controller must balance the variety of the system. In the Industrial age, our networks and communications gave rise to low control variety, thus we had to partition the battlespace into sectors, and have specialised force units, in order to reduce the variety of the battlespace, in accord with Ashby’s Law. Low variety of the physical battlespace was matched to low variety of the command process. Now as we move into the Information Age, we foresee a turbulent and uncertain set of futures, and a battlespace with high variety. Thus we need to construct a representation of the human command and decision-making process which gives rise to high variety (Atkinson and Moffat 2005). In my work I have captured this by creating two representations of human decision-making denoted Deliberate Planning and Rapid Planning. Rapid Planning, reacting fast to local circumstances, creates variety. This is then constrained by more strategic Deliberate Planning in order to produce the requisite variety of command.

The balance between ‘top down’ Deliberate Planning and the more emergent Rapid Planning changes as we progress to more mature levels of Command and Control. Figure1, taken from (Moffat and Alberts 2006) shows these maturity levels explicitly. De-conflicted C2 corresponds to the Industrial Age C2 we discussed earlier, while increasing levels of maturity take us towards the requirements for Information Age C2. These maturity levels can also be thought of as milestones on the NEC journey shown in Figure 2, progressing through the various ‘epochs’ of NEC as described in (UK MoD 2005).

At the highest maturity level for the employed force, Agile C2, such emergent Rapid Planning is constrained by broader shared awareness and shared intent rather than by Deliberate Planning, and capturing this type of C2 in our simulation models is the current focus of my research.

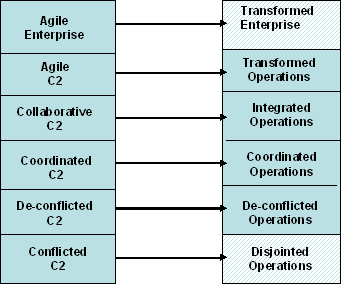
Figure 1: Increasing maturity levels of Command and Control and the corresponding operational levels which can be commanded.

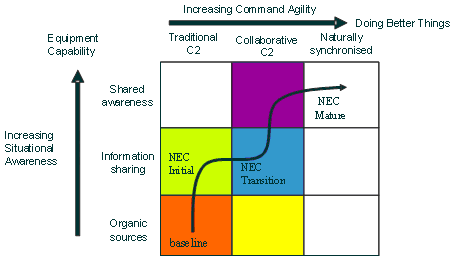
Figure 2: The NEC journey.

Building the Simulation Model Set

Now I want to show how these ideas have come together to form the basis of a number of linked closed form (constructive) simulation models, which underpin Dstl’s ability to offer advice on balance of investment across the equipment budget (including sensors and command systems), future force structures, and the implications of high level Defence policy (Taylor and Lane 2004).

Deliberate Planning represents decision-making based on a rational choice among alternatives. (In cybernetic terms it is a feedforward process). In such rational choice decision-making the emphasis is on the explicit generation, and subsequent evaluation, of alternative courses of action. In military terms it corresponds to the generation of a plan which involves the allocation of multiple forces both in space and time, in order to prosecute an intent and objectives. This is complemented by the Rapid Planning process (in cybernetic terms a feedback process), based on the psychological construct of naturalistic decision-making. In military terms, the emphasis is on making sense of the immediate situation, in a rapidly changing environment, and applying the decision-maker’s expert experience of similar situations stored in long term memory (and built up through training and experience) to jump directly to a workable solution. The situation is described by a number of cues, which define a ‘decision space’. The stored situations correspond to fuzzy regions in this decision space.

The mathematical algorithms which implement these two approaches to human decision-making are described in detail in (Moffat 2002). In summary, the approach I have adopted is to strike out on a new path, and exploit novel ideas from complexity mathematics in order to create a representation of the command process which is sufficient, yet still transparent. This avoids the use of extensive sets of special expert system rules (the previous available approach to such issues). Examples of the simulation models either developed or under development are:

The COMAND campaign level Maritime, Air and Land model. This is a Command and Control centred model which is based on the Rapid and Deliberate Planning processes. This model is the key component of Dstl studies looking at joint balance of capability (including C2) across the defence budget.

The DIAMOND model which represents non-warfighting scenarios at a joint level (including the effects of non-military entities such as refugees, or aid agencies) and exploits the agent architecture developed as part of my research. This model is now in use in studies, and has been given to a number of other countries, including the Defence Modelling and Simulation Office (DMSO) in the US.

The CLARION campaign level Land/Air model is due to incorporate the Rapid Planning process. CLARION is the main model within Dstl for analysis of Land/Air force structure tradeoffs across the equipment budget.

The SIMBAT model (providing underpinning analysis at the tactical level) is a pure instantiation of the Rapid Planning process. It typically represents a number of Companies under Battlegroup command and is used to support lower level studies as well as high level analysis.

The SIMBRIG model at Brigade level spans the gap between SIMBAT and CLARION. It has been developed using elements of the Rapid Planning process to drive the manoeuvre units.

The SIMMAIR Maritime/Air model is currently under development as a system level model to bridge the gap between tactical naval models and the COMAND model. It will be driven by the Rapid Planning process.

The WISE formation level wargame comprises a number of military players at up to Divisional and Brigade level, underpinned by a simulation ‘engine’. This engine is driven by the Rapid Planning process. I have recently developed a closed form simulation version of WISE, incorporating the Deliberate Planning process. The gaming structure is now in study use, and has been key to consideration of future UK Army operational level force structures.

All of these models (with the exception of WISE) are closed form (i.e., constructive) simulations. Figure 3 indicates how they fit together to form a hierarchy for application to analysis across the spectrum of requirements, and how these are shared and owned by the various Systems Departments in Dstl: Policy and Capability Studies (PCS), Air and Weapons Systems (AWS), Land Battlespace Systems (LBS) and Naval Systems (NS).

Figure 3: How these models fit together across the Systems Departments of Dstl.

Validation of Deliberate and Rapid Planning through Comparison with Historical Events

In this part of the paper, I want to give some examples of how these apparently rather abstract models do actually reflect key aspects of human decision-making by commanders in the field. Indeed, as part of transitioning such models to the study programme, they have to undergo a rigorous validation process. This includes both detailed scrutiny of the model assumptions and behaviour by military officers, and (where possible) comparison of the model behaviour with historical conflicts of relevance. For example, as part of the process of commissioning the COMAND model, a detailed comparison was made between COMAND and the Falklands conflict of 1982. The outputs we examined were the casualties suffered. Since these are essentially a product of the number of engagements, and the effectiveness per engagement; if we calibrate the comparison back to the effectiveness levels per engagement historically achieved, then this is a fair test of whether we are correctly modelling the number of engagements (an essential product of the decision-making process).

Since COMAND is a stochastic model this comparison was between the single actual outcome of the 1982 conflict, and the ‘fan’ of results from 160 replications of the COMAND model (Moffat, Campbell and Glover 2004). Three main types of agent decision-making were represented in this comparison: a). In terms of the (Deliberate) campaign plan for each side’s maritime assets, this consisted of a string of missions. At various points, triggers were built into the plan, allowing it to branch to a new string of missions dependent on the situation at the trigger point (this might be the sinking or not of a major warship for example). b). In terms of Rapid Planning, maritime missions could be adapted to reflect local circumstance. For example a UK ship in transit to a patrol area could mount an attack of opportunity if its sensors detected such a threat and the attack was likely to succeed. c). Air missions were developed and prosecuted as a function of the sensor information on targets. For example all Argentinean air missions attacking the UK task force were created by the model (i.e., were generated by the model, not by scripting) in response to sensor information (mainly from Maritime Patrol Aircraft (MPA) and sensors based on the Falkland Islands). We were thus able to explicitly represent both UK and adversary decision-making in the model.

Entity/group missions are the building blocks of the scenario and are the key to COMAND’s representation of human intelligence is represented by the decisions made by the various commanders, and the emergent effect of these decisions. Broadly it was possible to represent all types of mission: for example, the retreat of the Argentinean navy to port, following the loss of one of their ships; the regrouping of the various UK ships into a single amphibious landing force and its subsequent passage to San Carlos.

In terms of overall campaign outcome, we performed a number of comparisons of casualties (actual versus predicted by the model). The effectiveness per engagement was scaled back to 1982 levels in the model based on the historical records and log books in order to reflect the actual probability of a successful engagement given a set of circumstances. Thus (as discussed earlier) this comparison was a true test of the validity of our representation of the command and decision-making processes. Many detailed comparisons were carried out. Just one of these is shown here (Figure 4), comparing the actual historical record of the number of UK ships sunk or operationally rendered incapable, versus that predicted by the model. The result is convincingly close. The decision-making process represented in the model must thus be close to that which was used in practice in the historical campaign. This is of course just a single point estimate. As discussed in (Moffat, Campbell and Glover 2004), our models undergo a continuing process of refinement and scrutiny by both expert analysts and in-house military advisors.

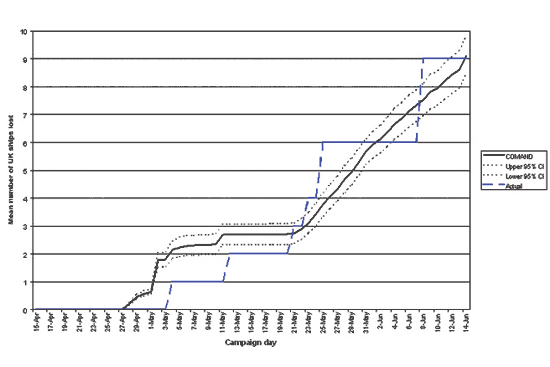
Figure 4: Comparison of the Falklands Conflict with the COMAND simulation.

COMAND is cross-environment and at the campaign level. As a contrasting example, SIMBAT is a tactical model of Army combat at the Battlegroup level. I was also able to show that with the inclusion of Rapid Planning, such tactical models begin to show the correct time and casualty dynamic associated with such tactical level warfighting. Previously, models at this level typically indicated a time of battle which was two or three times too short, due to lack of proper representation of the command process.

For example, consider the battle of Goose Green fought as part of the Falklands war between UK 2 PARA Battlegroup and a mixed force of Argentinean conscripts during 28/29th May 1982 (Moffat, Campbell and Glover 2004). The infantry battle started at midnight and finished at 20:00 the following evening. The Argentinean forces involved were approximately equal in number to the British. The British force was highly trained and motivated. However, they were fatigued from six days with little shelter on the slopes of Sussex mountain, and by an 18Km march to the battlefield with little sleep. They were also shocked by an air attack on their ammunition point prior to the march. The British troops were opposed by Argentinean conscripts with barely four months training and little motivation. They were, however, fresh for battle, although shocked from low-level tactical British overflights and surprised by the British move to attack. We discuss below how these human factors, together with the decision-making process, were modelled and how the results compared to the reality.

We represented the concept of overall ‘force strength’ in the SIMBAT model, as being composed of overall effectiveness. This was then factored by a number of constraining effects, namely; unit participation (i.e., the percentage of the force prepared to contribute to the battle), the effect of being shocked, the effect of being surprised, whether the troops were close combat trained, and their resilience to fatigue. The detailed quantitative assumptions are in (Moffat, Campbell and Glover 2004). This allowed us to define quantitatively, three categories of force; Strong, Medium and Weak, for both the British and Argentinean forces, which took account of all of these human factors effects. The SIMBAT model was then run for each of the 3x3 combinations of force on each side (taking an average of 30 simulation runs in each case, since the model is stochastic). Again, as for the COMAND model, considering casualties (actual versus predicted by the model) is a good way of testing whether the decision-making approach represented in the model accords with what happened in practice. The model shows that these human factors effects are a dominant determinant of the outcome. Modelling Strong to Medium British forces versus Weak Argentinean forces gave total casualty results (and hence a decision-making process) close to the historical record, as described in detail in (Moffat, Campbell and Glover 2004).

In the historical battle, there were a number of key objectives achieved by the British forces, and the times at which they were achieved were recorded. Thus it was possible to compare the model prediction of times to these objectives (again averaged over 30 runs of the model), with this historical record, as shown in Table 1 below.

Key Objective	Historical Record	Strong British v Weak Argentine	Medium British v Weak Argentine
Burntside house and hill secure	04:00	02:30	03:00
A Company at Coronation Point and B and D Companies through Northern Positions	06:30	04:30	04:30
A Company held at Darwin Ridge, B and D Companies held at Middle Hill	07:30	06:00	06:15
A Company take Darwin Ridge, B and D Companies take Boca House	10:30	10:45	11:15
Companies at their finish positions	17:00	18:30	19:15
Proportion total battle time deviates from actual historical record.	N/A	8%	13%

Table 1: Comparison of SIMBAT model times to achieve key objectives with the historical record.

The close correlation between the model results and the historical record again demonstrates that the Rapid Planning process representation of decision-making in SIMBAT must be close to the real decision-making process employed in the historical battle.

Validation of Rapid Planning Using Single Decision Gaming

Having now looked at these models of conflict in some detail, I want to turn now to some of the underpinning research. This also helps to demonstrate that our approach is anchored in real human effects.

We have extended the basic form of the Rapid Planning process using non-linear utility theory (Dodd, Moffat and Smith 2006), in order to help us to explain why decisions differ qualitatively dependent on the decision-makers’ experiences and preferences. More precisely we wish to understand:

How the objective inputs (based on incoming information) and the subjective inputs (based on an individual’s training, experience and personality) combine in the decision-making process.
How considerations of utility influence this process; in particular, when there are conflicting local and global values within the decision-making structure.

Theoretical Perspective

The missions described in our experimental situation are simplified to just two levels of attributes. The first set of attributes measures the local outcome of the mission in terms of relatively immediate, ‘close-to-home’ considerations (such as loss of tactical assets). The second set of attributes measures longer-term and more global concerns related to more strategic considerations (for example, integrity of the NATO campaign). Our analysis describes how this tension between local and global concerns can formally be modelled.

The choice of course of action depends on the interpretation of mission orders (i.e., weighing of priorities in terms of utilities) and the subjective situation assessment (i.e., weighing of evidence derived from subjective informational attributes). The commander may be unable simultaneously to reconcile, even partially, the objectives associated with the attributes pertaining to the high-level mission objectives and his own local appreciation of immediate potential threat. When this happens he may be forced to choose an action that focuses on local, shorter-term success, marginalising the longer-term implications of his action. Alternatively, he may place more weight on global concerns. This tension between objectives is the basis for the derivation of the subjective utility and depends on subjective descriptors of the conflict situation, interpretation of the mission orders, and general appreciation of the situation. The relative importance each commander places on local and global objectives is central to a conceptual understanding of ‘value’ in decision-making. It seems that such qualitative relationships are enduring in this context and that they provide a useful framework for C2 modelling.

In practice, most Bayesian decision analyses usually begin by assuming that the decision-maker’s utility function, U, has an associated set of value-independent ‘situation’ attributes (Keeny and Raiffa 1976). In our application, these attributes are associated with situation features that are immediately local to the decision-maker and those that have a longer-term, more global impact. For a decision, d, a decision-maker's utility function thus has to capture the trade-off between the different goals by assigning weights, to reflect the importance of achieving the desired values of the attributes, whose achievement is evaluated by the utilities. ( is a set of shape parameters describing his utility function).

Projected future values of the attributes are represented by a probability distribution function which reflects the decision-maker's current (subjective) probability of the outcome relative to the goal attribute , given decision d, where is a set of shape parameters for this probability distribution.

The decision-maker should thus choose d to maximise the utility function , averaging over his beliefs about different outcomes and their utilities. The decision-maker also implicitly sets weights reflecting, for instance, his priorities and ambitions. In military settings a decision-maker will be held accountable for his chosen course of action d. It is therefore reasonable to expect that the specific nature of the mission objectives and the previously absorbed general training and personal history will be reflected in the commander's setting of .

The Single Decision Game

A single decision game was thus designed to measure the predisposition of commanders, in a situation in which they should be experts, by requiring them to make a rapid determination of a course of action. Participants were presented with an initial operational picture and situation brief. Following ten minutes to appraise the situation, an Intelligence report was briefed which might (or might not) demand action. The participants were then asked to choose and write down a course of action without being given further time for analysis. The Intelligence update was designed to give them some room for choosing different courses of action so that their pre-dispositions were allowed to surface as variations in choice.

After the course of action was selected, participants were invited to record their situation appraisal and assessments along with the key indicators considered relevant to their course of action choice. It was accepted that this data might reflect post-hoc rationalisation to some extent. To account for any changes in situation assessment due to the process of having to analyse and express it, the participants were also offered the opportunity to record any other courses of action that they may have considered. The experimental game results give us a context within which to explore and test our non-linear utility theory; in particular, the ways in which individuals’ predispositions affect the weights given to the situational attributes. It appears that the extent to which each attribute is (or is not) considered in the pattern-matching process of Rapid Planning strongly determines the choice of course of action. The experimental game was based on decisions at Battlegroup and Company levels set in two different conflict scenarios: war-fighting and peace-support.

War-Fighting Scenario

The war-fighting game was played after participants had taken part in a related Brigade-level planning exercise, forming part of a broader series of games organised by Graham Mathieson of Dstl, examining all of the factors bearing on the decision-making process. This provided them with a good appreciation of the operational context. The participants were focused on a decision concerning a Battlegroup (BG) of three tank Companies located in hides on a large wooded ridge feature called Elfas (circled top middle-left in Figure 5). Enemy armoured and mechanised units could be seen travelling along roads either side of the ridge. The Brigade’s mission was to delay the enemy’s advance for twenty-four hours until bridges to the West could be secured. A full written brief was presented that described the current operational status of all units within the Brigade’s area of interest. Then followed a situation update as depicted in Figure 5.

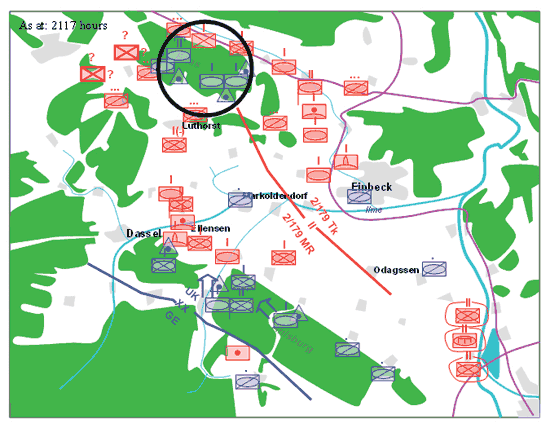
Figure 5: Situation Update for the Warfighting Scenario.

The situation update indicates probable enemy airborne deployments to the West of the Elfas feature. The strength of these deployments is not known but is assessed as an augmented Company. The participants were asked to write down immediately their course of action. As the BG commander in the field HQ there are several courses of action available, for example:

remain in hides and do nothing;
request more information;
attack North/North-East (hoping for surprise) against the armoured enemy units;
attack West directly against the reported deployment of airborne troops;
maintain a South-East withdrawal route to join-up with own forces.

The decisions taken across the twenty-four participants (all UK army officers) appear to vary according to the way that they have taken account of the situation attributes and the higher-level mission orders. Some participants choose to give very little (if any) weight to the higher-level mission orders and focus on achieving effects that satisfy local utility. This local view of the mission in some cases tends to extend to the use and interpretation of the situation attributes in terms of both space and time. For example, the situation may be appraised purely as a snapshot in time (i.e., little or no forward projection) so that decision outcomes are assessed only from the point of view of the BG, ignoring the overall Brigade mission.

The analysis reveals two concurrent, inter-dependent assessment processes: threat and risk assessment. For those participants who are not so concerned about the uncertainty in the situation update, the relative weightings of the BG and Brigade mission priorities coupled with the practical consideration of employing tanks against dismounted airborne troops, result in two very different courses of action. Some choose to attack West (employing tanks against dismounted troops and preventing link-up and closure of the gap West of Luthorst) while others choose to attack North/N-East using tanks against tanks and adhering to Brigade orders. Where there is uncertainty and lack of confidence, the participants choose either to keep tanks in reserve; or prepare for attack while doing further reconnaissance; or secure a withdrawal route to rejoin the southern BG; or simply do nothing, remain in hides and report to Brigade. There is further discussion of these alternatives and their motivation in (Dodd, Moffat and Smith 2006).

Peace-Support Scenario

The peace-support scenario was set in a fictitious federation and involved provision of armed support for conveyance of supplies and civilians to and from a NATO-protected enclave East of the ‘Nettoyer Pass’, as shown in Figure 6.

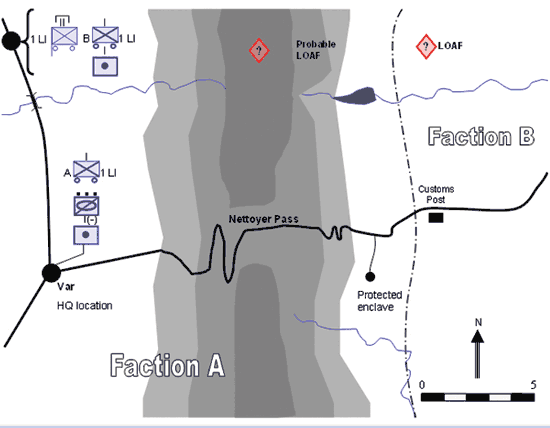
Figure 6: Peace-Support Scenario.

Following the break-up of the federation, the two major factions were left in a state of armed stand-off. The NATO Task Force, with the UK acting as the lead nation, was a Division-sized force with the task of disarming the ethnic militia. NATO forces also had undertaken to escort and protect all aid convoys. The broader NATO mission was to restore peace and stability to the area in order to create the conditions for a free vote by the population on the future of the region.

The Intelligence update was sent to the tactical commander in the form of a radio message from an armed unit with two Land Rovers escorting a civilian relief convoy of six vehicles. The armed convoy was stopped at a probable Illegal Vehicle Control Point (IVCP) in a mountain pass as it returned from delivering supplies to the enclave. The IVCP consisted of twelve men, armed with AK-47 assault rifles and at least two RPG-7’s. The second escort Land Rover was 500m to the rear of the convoy. We focus here on the decision-making of the commander at the field HQ located at Var (see Figure 6). There are several courses of action available; for example:

Order the UK troops to negotiate their way out of the situation;
Order a withdrawal to move the civilian convoy vehicles to a safe distance;
Do nothing and hope that the militia let the unit and convoy through eventually;
Deploy the quick reaction force (QRF) and move artillery units to fire positions.

There are well-defined NATO rules of engagement: for example, personal, direct-fire and indirect-fire weapons may be used to engage a positively identified threat.

Here the immediate potential outcomes of the mission are measured against attribute and scored by utility function . This evaluates features that have consequences local to the situation, such as an escalation of the immediate threat by ambush or weapon-firing, the reduced security of the civilians in the convoy and likelihood of kidnap, theft of supplies, etc. The second attribute is scored by , evaluating more global issues concerning, for example, the integrity of the NATO campaign and political perceptions of NATO’s ability to show resolve while adhering to the rules of engagement. The nature of peace-support operations generally means that the command structure tends to be flatter and with a less explicit hierarchy of mission orders (in contrast to the war-fighting scenario). Therefore we would expect the course of action selection to be driven more from the situation attributes than from the weighting of mission priorities.

The decision model then is as follows:
is the subjective priority weighting of local effects.
is the subjective priority weighting of global effects .
is the utility of the decision with respect to local outcomes.
is the utility of the decision with respect to more strategic consequences.
is a vector of shaping parameters for the subjective distribution of probable outcomes, and represents the general level of the commander’s uncertainty in the situation.

The local features for attribute typically concern the potential for:

Escalation of threat (in particular an ambush or firing of weapons);
Loss of civilian life;
Own force casualties;
Theft of convoy assets;
Taking of hostages.

The global features for attribute are typically:

Show of strength against NATO resolve to restore stability;
Provocation to create over-reaction and heightened regional tension.

In order to plot in two dimensions the participants’ decision space, the features are combined into two measures that represent the seriousness of the terrorist threat and the sense of provocation through a show of strength. The former reflects the indications for ambush and imminent need to address a real threat with direct force. The latter measure embodies the features concerned with the need to avoid escalation. We can then plot the participants’ situation assessments in this two-dimensional decision space (Dodd, Moffat and Smith 2006). Overlaid onto this situation assessment plot is the grouping of the participants into their course of action choices. They form coherent areas in the decision space. This shows how the pattern matching process of Rapid Planning leads directly to a choice of course of action.

Based on the results of these games, the Rapid Planning process representation has been extended to include weightings on the cues which span the decision space, and utility curves similar to those of Prospect Theory (Kahneman and Tversky 1979) which represent the utility of a cue value given a particular course of action. Thus for a given cue j, we define a weight , with , and . For each cue j with outcome values , and each course of action d, we also define a non-linear utility curve . The cue value at any given point in time will have an uncertainty associated with it, and thus a probability distribution of values . We combine these together to obtain the overall utility . We then sum this over all cues to obtain the overall utility of the course of action d as follows:

In the extended form of the Rapid Planning process, this is used to choose between a course of action which is consistent with higher level orders, and one which is locally more appropriate (through comparing their relative utilities). Implementation in the HiLOCA model shows encouraging results (see for example (Dodd, Richardson and Alston 2006)).

Validation of Rapid Planning Using Card Based Decision Games

Recently, we have examined the decision-making of CBRN Commanders using experimental gaming (Moffat, Medhurst and Tilley 2007). These decision games have allowed statistical models of their decision-making behaviour to be developed that are able to significantly predict the probability of making a given command choice, given the information presented to the commander, accounting for 60% to 80% of the variance in outcome. The statistical models imply that the decision-making is of the form implied by the Rapid Planning process, as we shall see. They involve a decision space (defined by a number of weighted information cues) and a number of discrete regions in this space corresponding to the decision options (alternative courses of action). As information about the cues is updated, the estimate of the position in the decision space is updated, leading to a potential change of course of action.

Two cases were considered. In the first the commander had to decide whether to issue a ‘precautionary alert’ to troops in theatre, leading to the donning of protective clothing, or whether to declare a ‘probable attack’, including the taking of medical countermeasures and reporting to higher command of a probable biological attack. This decision was based on information from sensors (e.g., the possible detection of a biological agent), and other contextual data (such as casualty reports, or shifts in weather patterns). It was thus essentially a single decision process, based on accumulating information. In the second set of decision games, the commander had to decide on the protective dress state for the force, and whether or not to continue advancing, based on prevailing information. He could raise or lower the dress state of the force a number of times during the game, based on the accumulating information as the game progressed. There were three choices: Dress State 1 (DS1), Dress State 2 (DS2), and Dress State with respirator (DSR). In the decision game, raising the dress state gave more protection, but slowed the force down.

In each game, information was presented to the commander using cards. These were of different types, corresponding to different classes of information. The cards were presented one by one, and the commander wove these together in his mind to form a ‘story’ of the unfolding scenario. The cards were presented in essentially random order (thus there was no pre-scripting of the set of events).

Statistical analysis of the data from the first set of games (the single decision games), shows that a probit analysis gives an extremely good fit to the data. Thus our model of the process is as follows.

There are three possible actions the commander can take:

j=0 (no alert issued);
j=1 (precautionary alert issued) ;
j=2 (probable attack issued).

038
039
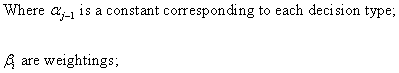
is the number of cards revealed of information type i;
is the cumulative distribution of the standard normal distribution N(0,1).
Thus we have the picture shown in Figure 7.

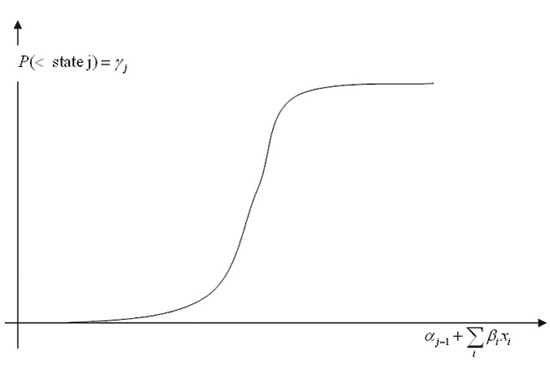
Figure 7: The relationship between being in less that state j, and the incoming information.

The decision to move to state j can thus be represented by the following statistical model.

Define

The probability of being in at least state j is thus given by:

The picture we drew earlier thus becomes Figure 8.

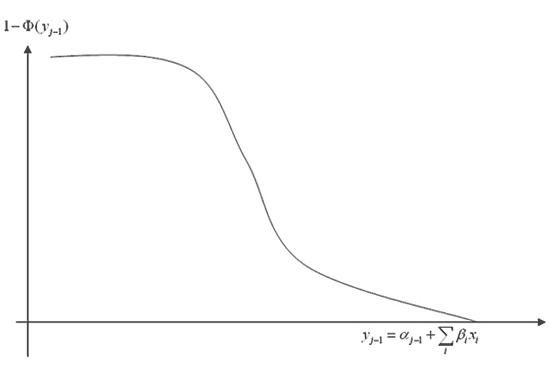
Figure 8: The relationship between the probability of being in at least state j, and the incoming information.

We should then note that the weights turn out to be all negative, so that as the number of cards of a given type increases, we are moving towards the origin of the x- axis, and thus ‘climbing up the probability slope of the logistic transform’ (i.e., the probability is increasing).

In terms of a decision process, we can thus illustrate this as shown in Figure 9, where the value 0.5 is illustrative, and where there are only two information types.

We define two regions in Figure 9. The first (Region A) corresponds to the set of values (i.e., the number of cards of each of the two information types which have already been shown to the commander), and for which the probability is . This corresponds to the region of the decision space within which the commander would choose the course of action ‘issue precautionary alert or higher’. The second region (Region B) is the subset of Region A corresponding to the set of values for which the probability is . This corresponds to the region within which the commander would choose the course of action ‘issue probable attack warning’.

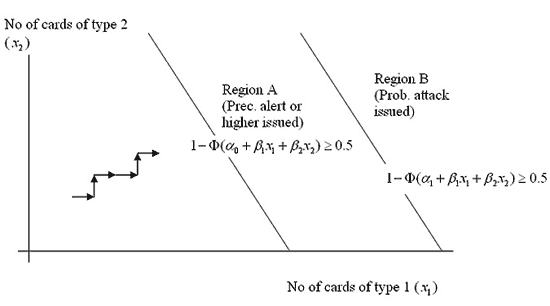
Figure 9: How the changing values of the cues (the numbers of cards of each information type) affects the decision taken.

The cues of the decision process are thus the different information categories in this case, and they are weighted by the constants . The regions corresponding to the different decisions are represented probabilistically, corresponding to fuzzy membership functions (as in the Rapid Planning process itself (Moffat 2002)). Overall, this simple model, where the cues correspond to the information types, can account for 60% of the variability in Pr (probable attack issued) (Pj=2), and 80% of the variability in Pr (precautionary alert or higher issued) (Pj=1). This obviously gives confidence that the model is representing a significant element of the real decision-making process.

An analysis of the second game (which allowed movement between the three states DS1, DS2 and DSR) shows that the commanders’ decisions can be captured in a similar way, and in fact form a simple Markov process, which is also to be expected from Rapid Planning considerations (Moffat 2002).

In each case, then, the statistical model which explains the commanders’ decision-making process is the Rapid Planning process (to an acceptable level of approximation), and is thus a relatively simple probabilistic model, rather than one based on complex, embedded and deterministic decision rules.

A key contributor to the residual unexplained variation in our statistical model is due to the intrinsic difference between each pair of players. Thus capturing more of this variation would involve explicitly representing this difference in personality, training and experience.

An Assessment and the Way Forward

The simulation models which we have built, incorporating these concepts of decision-making at their core, represent a significant monetary and intellectual investment by the UK MoD. This investment has yielded significant improvements in our ability to systematically address a number of issues related to the development of NEC. As described in detail earlier, the Rapid Planning process and aspects of the Deliberate Planning process have been implemented in a number of these models. They are thus sufficient to take us along the journey from our current capabilities to the ‘NEC Transition’ epoch of NEC (UK MoD 2005) as shown in Figure 2.

However, our understanding of Agile C2 and the Mature stage of NEC, envisaged as towards the end of the NEC journey, are still not sufficient for the full development of tools and methods by which they can be modelled. A key shortcoming is our relative inability to model the agility of task organised force units. I am thus continuing to work on enhancing both our conceptual understanding, and the model set, to capture these ideas.

This requires a proper representation, in the constructive simulation environment, of how ‘edge organisations’ (Alberts and Hayes, 2004) share situational awareness (including command intent) and constrain the emergent behaviour of a number of interacting entities in order to produce the natural synchronisation indicated in Figure 2. It also requires the ability, with Agile C2, to shape and adapt the C2 approach to the changing circumstances in a timely manner.

Acknowledgements

The contributions of Lorraine Dodd (Qinetiq), John Medhurst (SCS), Professor J Smith (Warwick University) and Paul Glover (Dstl) to the thoughts in this paper are gratefully acknowledged. I would also like to acknowledge the help, guidance and support which I have received from Geoff Hawkins, who has sponsored much of the work described here.

Footnotes

Chemical, Biological, Radiological and Nuclear.
The word Cybernetics was first used by Ampere as the title of a sociological study. It is derived from the Greek work for steersman.

References

Alberts D and Hayes R. 2004. Power to the edge. Washington, DC: DoD CCRP.
Atkinson S and Moffat J. 2005. The agile organization. Washington, DC: DoD CCRP.
Dodd L, Moffat J, and Smith J. 2006. Discontinuity in decision-making when objectives conflict: A military command decision case study. J Opl Res Soc 57 643-654.
Dodd L, Richardson S, and Alston A. 2006. Results from C2 modelling and simulation for edge organizations. Proceedings of 11th ICCRTS, Cambridge, UK.
Kahneman D and Tversky A. 1979. Prospect theory: An analysis of decision under risk. Econometrica.
Keeny R and Raiffa H. 1976. Decisions with multiple objectives. New York, NY: Wiley.
Moffat J and Alberts D. 2006. Maturity levels for NATO NEC command. Dstl Unpublished Report.
Moffat J, Medhurst J, and Tilley D. 2007. Modelling human decision-making and improving rapid planning using experimental gaming. Dstl Unpublished Report.
Moffat J. 2002. Command and control in the information age: Representing its impact. London, UK: The Stationery Office.
Moffat J, Campbell I, and Glover P. 2004. Validation of the mission-based approach to representing command and control in simulation models of conflict. J Opl Res Soc 55, 340-349.
Taylor B and Lane A. 2004. Development of a novel family of military campaign simulation models. J Opl Res Soc 55, 333-339.
UK MoD. 2005. The JCB NEC delivery strategy, Final Version.
Weiner N. 1948. Cybernetics. USA: Technology Press and John Wiley.